Линейное гауссово условное распределение обладает некоторыми особыми свойствами. Сеть, содержащая только непрерывные переменные с линейными гауссовыми распределениями, имеет совместное распределение, представляющее собой многомерное гауссово распределение по всем переменным нескольких измерениях, которая имеет пик в районе среднего значения, в η измерениях, и уменьшается по всем направлениям.) Если в сеть введены дискретные переменные (при условии, что ни одна дискретная переменная не является дочерней применительно к непрерывной переменной), то сеть определяет условное гауссово распределение, или распределение CG (conditional Gaussian): если дано любое присваивание дискретным переменным, то распределение по непрерывным переменным становится многомерным гауссовым распределением.

Теперь обратимся к распределениям для дискретных переменных с непрерывными родительскими переменными. Например, рассмотрим вершину Buys на рис. 14.5. Представляется обоснованным предположение, что клиент сделает покупку, если стоимость является низкой, и не сделает покупку, если она высока, а также, что вероятность покупки изменяется плавно в некотором промежуточном регионе. Другими словами, условное распределение напоминает "мягкую" пороговую функцию. Один из способов определения мягких пороговых функций состоит в использовании интеграла стандартного нормального распределения:

В таком случае вероятность события Buys, если дано значение Cost, может выражаться следующей формулой:

которая означает, что пороговое значение стоимости обнаруживается в районе μ, ширина порогового региона пропорциональна σ, а вероятность покупки уменьшается по мере возрастания стоимости.

Такое распределение вероятностей называется пробит-распределением (probit distribution) и показано на рис. 14.7, а. Возможность применения распределения с такой формой может быть обосновано тем, что соответствующий процесс принятия решения имеет твердый порог, но точное расположение этого порогового значения подвержено воздействию случайного гауссового шума. Альтернативным по отношению к пробит-распределению является логит-распределение (logit distribution), в котором для формирования мягкого порога используется сигмоидальная функидя (sigmoid function):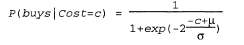