|
Страница 7 из 14 Выше было показано, что игра может иметь больше одного равновесия Нэша; но на основании чего мы можем утверждать, что каждая игра должна иметь по меньшей мере одно такое равновесие? Может оказаться, что в игре отсутствует равновесие Нэша для чистой (не смешанной) стратегии. Рассмотрим, например, любой профиль чистых стратегий для игры в чет и нечет на двух пальцах (с. 839). Если общее количество показанных пальцев является четным, то игрок О может захотеть переключиться на другую стратегию, а если это количество нечетно, то будет стремиться переключиться игрок е. Поэтому ни один профиль чистых стратегий не может представлять собой равновесие и приходится рассматривать смешанные стратегии. Но какой должна быть смешанная стратегия? В 1928 году фон Нейман разработал метод поиска оптимальной смешанной стратегии для игр с двумя игроками, называемых играми с нулевой суммой. Игрой с нулевой суммой называется игра, в которой вознаграждения в каждой ячейке матрицы вознаграждения в сумме равны нулю. Очевидно, что игра в чет и нечет является именно таковой. Известно, что для игр с двумя игроками и нулевой суммой вознаграждения являются равными и противоположными, поэтому достаточно рассмотреть вознаграждения только для одного игрока, который будет считаться максимизирующим игроком (точно так же, как и в главе 6). Применительно к игре в чет и нечет выберем в качестве максимизирующего игрока Е, который выбрал для себя в качестве выигрышного результата четное количество пальцев, поэтому можно определить матрицу вознаграждений на основе значений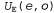 — вознаграждение, получаемое игроком Е, если игрок Ε выбирает действие е, а О — действие о. — вознаграждение, получаемое игроком Е, если игрок Ε выбирает действие е, а О — действие о. Метод фон Неймана называется методом максимина и действует, как описано ниже. • Предположим, что правила игры изменились таким образом, что игрок Ε вынужден раскрывать свою стратегию первым, а за ним следует игрок О. В таком случае мы имеем дело с игрой, где ходы выполняются поочередно, к которой можно применить стандартный минимаксный алгоритм из главы 6. Допустим, что такая игра приводит к получению результата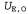 . Очевидно, что эта игра окончится в пользу игрока О, поэтому истинная полезность U данной игры (с точки зрения игрока Е) равна по меньшей мере . Очевидно, что эта игра окончится в пользу игрока О, поэтому истинная полезность U данной игры (с точки зрения игрока Е) равна по меньшей мере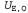 . Например, если рассматриваются только чистые стратегии, то минимаксное дерево игры имеет корневое значение, равное -3 (рис. 17.9, а), поэтому известно, что . Например, если рассматриваются только чистые стратегии, то минимаксное дерево игры имеет корневое значение, равное -3 (рис. 17.9, а), поэтому известно, что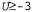
|