Если множество разрыва цикла имеет размер с, то общее время прогона алгоритма составляет 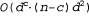. В том случае, если граф по своей форме "очень близок к дереву", то множество с будет небольшим, а экономия времени по сравнению с прямым поиском с возвратами окажется огромной. Но в наихудшем случае количество элементов с может достигать (п-2). Задача поиска наименьшего множества разрыва цикла является NP-трудной, но известно несколько эффективных алгоритмов решения этой задачи. В целом данный алгоритмический подход носит название определения условий выбора множества разрыва цикла (cutset conditioning); мы снова столкнемся с этим понятием в главе 14, где оно используется при формировании рассуждений о вероятностях.

Второй подход основан на формировании древовидной декомпозиции (tree decomposition) графа ограничений и создании множества связанных подзадач. Каждая подзадача решается независимо, а затем итоговые решения комбинируются. Как и большинство алгоритмов, действующих по принципу "разделяй и властвуй", этот алгоритм работает успешно, если подзадачи не слишком велики. На рис. 5.8 показана древовидная декомпозиция задачи раскрашивания карты на пять подзадач. Любая древовидная декомпозиция должна удовлетворять трем приведенным ниже требованиям.

•    Каждая переменная из первоначальной задачи появляется по меньшей мере в одной из подзадач.

•    Если две переменные первоначальной задачи связаны ограничением, то должны появиться вместе (наряду с этим ограничением) по меньшей мере в одной из подзадач.

•    Если какая-то переменная появляется в двух подзадачах в дереве, то должна появляться в каждой подзадаче вдоль пути, соединяющего эти подзадачи.

Первые два условия гарантируют, что в декомпозиции будут представлены все переменные и ограничения. Третье условие на первый взгляд кажется довольно формальным, но просто отражает то ограничение, что любая конкретная переменная должна иметь одно и то же значение в каждой подзадаче, в которой появляется; соблюдение этого ограничения гарантируют связи, соединяющие подзадачи в дереве. Например, переменная SA появляется во всех четырех связанных подзадачах на рис. 5.8. На основании рис. 5.7 можно убедиться, что эта декомпозиция имеет смысл.