Это выражение можно вычислить, последовательно обрабатывая в цикле его переменные и перемножая в ходе этого элементы таблицы СРТ. При каждом суммировании необходимо также выполнить цикл по возможным значениям переменной. Структура этих вычислений показана на рис. 14.8. Используя числа, приведенные на рис. 14.2, получим выражение. Соответствующее вычисление дляприводит к получению выражения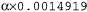, поэтому имеет место следующее:

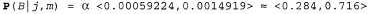
Таким образом, вероятность взлома, при условии, что поступили звонки от обоих соседей, составляет около 28%.

Процесс вычисления выражения, приведенного в уравнении 14.3, показан в виде дерева синтаксического анализа выражения на рис. 14.8. В алгоритме Enumeration-Ask, приведенном в листинге 14.1, вычисление подобных деревьев осуществляется с использованием рекурсии в глубину. Таким образом, пространственная сложность алгоритма Enumeration-Ask зависит от количества переменных только линейно; по сути этот алгоритм вычисляет суммы по полному совместному распределению, даже не формируя его явно. К сожалению, его временная сложность для сети с η булевыми переменными всегда составляет; это лучше по сравнению с оценкойдля простого подхода, описанного выше, но все еще довольно велика. В отношении дерева, приведенного на рис. 14.8, необходимо сделать еще одно замечание — в нем явно показаны повторяющиеся подвыражения, вычисляемые с помощью этого алгоритма. Произведениявычисляются дважды, по одному для каждого значения е. В следующем разделе описан общий метод, позволяющий избежать таких избыточных вычислений.

Листинг 14.1. Алгоритм перебора для получения ответов на запросы в байесовских сетях

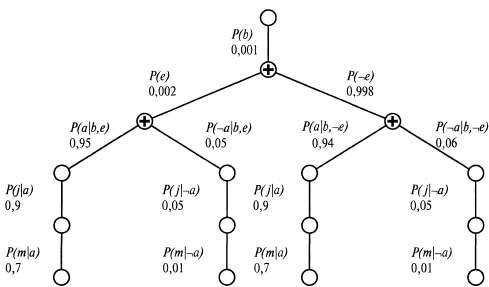
Рис. 14.8. Структура выражения, показанного в уравнении 14.3. Процесс вычисления осуществляется сверху вниз; при этом значения вдоль каждого пути умножаются и суммируются в узлах "+". Обратите внимание на то, что пути для j и m повторяются