По аналогии с минимаксными значениями, очевидный подход к использованию ожидаемых минимаксных значений состоит в том, чтобы останавливать поиск в некоторой точке и применять функцию оценки к каждому листу. На первый взгляд может показаться, что функции оценки для таких игр, как нарды, должны быть полностью подобными функциям оценки для шахмат, ведь от них требуется лишь то, чтобы они присваивали более высокие оценки лучшим позициям. Но в действительности наличие узлов жеребьевки означает, что требуется более тщательный анализ смысла таких оценочных значений. На рис. 6.10 показано, что происходит в играх с элементами случайности — при использовании функции оценки, которая присваивает листьям значения [1,2,3,4], наилучшим является ход А1, а если присваиваются значения [1,20,30,400], наилучшим становится ход А2. Поэтому программа ведет себя полностью по-разному, если вносятся изменения в шкалу некоторых оценочных значений! Как оказалось, такой чувствительности к изменению шкалы можно избежать при условии, что функция оценки представляет собой положительную линейную трансформацию вероятности выигрыша из некоторой позиции (или, в более общем смысле, ожидаемой полезности данной позиции). В этом состоит важное и общее свойство ситуаций, связанных с наличием неопределенности, и это свойство дополнительно рассматривается в главе 16.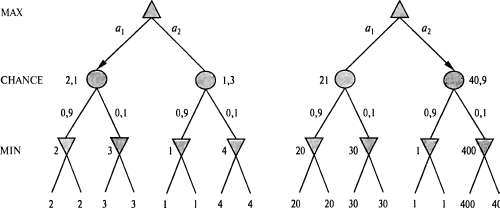

Рис. 6.10. Пример того, что в результате трансформации оценочных значений аистъев, при которой не изменяется упорядочение этих значений, наилучший ход становится другим