|
Страница 3 из 5 Каждое решение должно представлять собой полное присваивание и поэтому должно находиться на глубине л, если имеется п переменных. Кроме того, дерево поиска распространяется только на глубину п. По этим причинам для решения задач CSP широко применяются алгоритмы поиска в глубину (см. раздел 5.2). К тому же такие задачи характерны тем, что сам путь, по которому достигается некоторое решение, не представляет интереса. Поэтому может также использоваться формулировка с полным состоянием, в которой каждое состояние представляет собой полное присваивание, удовлетворяющее или не удовлетворяющее ограничениям. На основе такой формулировки хорошо действуют методы локального поиска (см. раздел 5.3). Задачи CSP простейшего вида характеризуются тем, что в них используются переменные, которые являются дискретными и имеют конечные области определения. К такому виду относится задача раскраски карты. Задача с восемью ферзями, описанная в главе 3, также может рассматриваться как задача CSP с конечной областью определения, где переменные 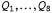 представляют собой позиции каждого ферзя на столбцах 1,...,8, а каждая переменная имеет область определения {1,2,3,4,5,6,7,8}. Если максимальный размер области определения любой переменной в задаче CSP равен d, то количество возможных полных присваиваний измеряется величиной представляют собой позиции каждого ферзя на столбцах 1,...,8, а каждая переменная имеет область определения {1,2,3,4,5,6,7,8}. Если максимальный размер области определения любой переменной в задаче CSP равен d, то количество возможных полных присваиваний измеряется величиной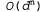 , т.е. зависит экспоненциально от количества переменных. К категории задач CSP с конечной областью определения относятся булевы задачи CSP, в которых переменные могут иметь значения либо true, либо false. Булевы задачи CSP включают в качестве частных случаев некоторые NP-полные задачи, такие как 3SAT (см. главу 7). Поэтому в худшем случае нельзя рассчитывать на то, что мы сможем решать задачи CSP с конечной областью определения за время меньше экспоненциального. Но в большинстве практических приложений алгоритмы CSP общего назначения позволяют решать задачи, на несколько порядков величины более крупные по сравнению с теми, которые могут быть решены с помощью алгоритмов поиска общего назначения, представленных в главе 3. , т.е. зависит экспоненциально от количества переменных. К категории задач CSP с конечной областью определения относятся булевы задачи CSP, в которых переменные могут иметь значения либо true, либо false. Булевы задачи CSP включают в качестве частных случаев некоторые NP-полные задачи, такие как 3SAT (см. главу 7). Поэтому в худшем случае нельзя рассчитывать на то, что мы сможем решать задачи CSP с конечной областью определения за время меньше экспоненциального. Но в большинстве практических приложений алгоритмы CSP общего назначения позволяют решать задачи, на несколько порядков величины более крупные по сравнению с теми, которые могут быть решены с помощью алгоритмов поиска общего назначения, представленных в главе 3. Дискретные переменные могут также иметь бесконечные области определения, например, такие, как множество всех целых чисел или множество всех строк. В частности, при календарном планировании строительных работ дата начала каждой работы представляет собой переменную, а ее возможными значениями являются целочисленные интервалы времени в сутках, отсчитываемые от текущей даты. При решении задач с бесконечными областями определения больше нет возможности описывать ограничения, перечисляя все допустимые комбинации значений. Вместо этого должен использоваться язык ограничений. Например, если работа Job1 которая занимает пять дней, должна предшествовать работе Job3, то для описания этого условия потребуется язык ограничений, представленных в виде алгебраических неравенств, таких как 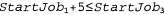 . Кроме того, больше нет возможности решать такие ограничения, просто перечисляя все возможные присваивания, поскольку количество подобных возможных присваиваний бесконечно велико. Для линейных ограничений с целочисленными переменными (т.е. ограничений, подобных только что приведенному, в которых каждая переменная представлена только в линейной форме) существуют специальные алгоритмы поиска решений (которые здесь не рассматриваются). Можно доказать, что не существует алгоритмов решения общих нелинейных ограничений с целочисленными переменными. В некоторых случаях задачи с целочисленными ограничениями можно свести к задачам с конечной областью определения, устанавливая пределы значений всех этих переменных. Например, в задаче планирования можно установить верхний предел, равный общей продолжительности всех работ, которые должны быть запланированы. . Кроме того, больше нет возможности решать такие ограничения, просто перечисляя все возможные присваивания, поскольку количество подобных возможных присваиваний бесконечно велико. Для линейных ограничений с целочисленными переменными (т.е. ограничений, подобных только что приведенному, в которых каждая переменная представлена только в линейной форме) существуют специальные алгоритмы поиска решений (которые здесь не рассматриваются). Можно доказать, что не существует алгоритмов решения общих нелинейных ограничений с целочисленными переменными. В некоторых случаях задачи с целочисленными ограничениями можно свести к задачам с конечной областью определения, устанавливая пределы значений всех этих переменных. Например, в задаче планирования можно установить верхний предел, равный общей продолжительности всех работ, которые должны быть запланированы.
|