Условное распределение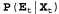называется моделью восприятия (или иногда моделью наблюдения), поскольку оно показывает, как фактическое состояние мира влияет на "результаты восприятия", т.е. на переменные свидетельства. Обратите внимание на то, каково направление зависимости: "стрелки" идут от состояния к значениям результатов восприятия, поскольку именно состояние мира вынуждает результаты восприятия приобретать данные конкретные значения. Например, в мире задачи с зонтиком дождь вынуждает директора прийти с зонтиком. (Разумеется, процесс вероятностного вывода проходит в другом направлении; одним из преимуществ байесовских сетей является то, что они позволяют провести различие между направлением моделируемых зависимостей и направлением вероятностного вывода.)

Кроме модели перехода и модели восприятия, необходимо определить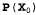—распределение априорных вероятностей состояний во время 0. Эти три распределения, в сочетании с предположениями об условной независимости, приведенными в уравнениях 15.1 и 15.2, позволяют получить спецификацию полного совместного распределения по всем переменным. Для любого конечного значения t получаем следующее: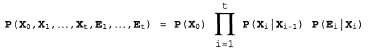

Предположения о независимости соответствуют очень простой структуре байесовской сети, описывающей всю систему. На рис. 15.2 показана структура сети для примера с зонтиком, включая условные распределения для модели перехода и модели восприятия.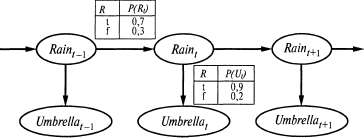

Рис. 15.2. Структура байесовской сети и распределения условных вероятностей, которые описывают мир задачи с зонтиком. Моделью перехода служит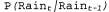, а моделью восприятия является

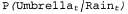
В структуре, показанной на этом рисунке, предполагается использование марковского процесса первого порядка, поскольку считается, что вероятность дождя зависит только от того, был ли дождь в предыдущие сутки. Является ли такое предположение обоснованным, зависит от самой проблемной области. Марковское предположение первого порядка указывает, что переменные состояния содержат всю информацию, необходимую для описания распределения вероятностей для следующего временного среза. Иногда такое предположение полностью соответствует истине; например, если некоторая частица совершает случайное блуждание вдоль оси х, изменяя свою позицию на величину ±1 в каждый интервал времени, то применение в качестве состояния координаты χ позволяет определить марковский процесс первого порядка. Иногда такое предположение является лишь приблизительным, как и в случае предсказания дождя лишь на основании того, был ли дождь в предыдущие сутки. Как описано ниже, существуют два возможных метода корректировки, если такое приближение оказывается слишком неточным.