Листинг 5.2. Алгоритм проверки совместимости дуг АС-3. После применения алгоритма АС-3 либо каждая дуга является совместимой, либо некоторая переменная имеет пустую область определения, указывая на то, что эту задачу CSP невозможно сделать совместимой по дугам (и поэтому данная задача CSP не может быть решена). Обозначение "АС-3" предложено разработчиком данного алгоритма [967], поскольку это — третья версия, представленная в его статье

Поскольку задачи CSP включают задачу 3SAT в качестве частного случая, не следует рассчитывать на то, что удастся найти алгоритм с полиномиальной временной сложностью, позволяющий определить, является ли данная конкретная задача CSP совместимой по дугам. Таким образом, можно сделать вывод, что метод проверки совместимости дуг не позволяет обнаружить все возможные несовместимости. Например, как показано на рис. 5.1, частичное присваивание {WA=red,NSW=red} несовместимо, но алгоритм АС-3 не обнаруживает такую несовместимость. Более строгие формы распространения ограничения можно определить с помощью понятия k-совместимости. Задача CSP является к-совместимой, если для любого множества к-1 переменных и для любого совместимого присваивания значений этим переменным любой к-й переменной всегда можно присвоить некоторое совместимое значение. Например, 1-совместимость означает, что совместимой является каждая отдельная переменная сама по себе; это понятие называют также совместимостью узла. Далее, 2-совместимость — то же, что и совместимость дуги, а 3-совместимость означает, что любая пара смежных переменных всегда может быть дополнена третьей соседней переменной; это понятие именуется также совместимостью пути.

Любой граф называется строго k-совместимым, если он является к-совместимым, а также (к-1)-совместимым, (к-2)-совместимым, ... и т.д. вплоть до 1-совместимого. Теперь предположим, что имеется некоторая задача CSP с узлами л, которая сделана строго n-совместимой (т.е. строго k-совместимой для к=п). Тогда эту задачу можно решить без возвратов. Для этого вначале можно выбрать совместимое значение для хi. В таком случае существует гарантия, что удастся выбрать значение для х2, поскольку граф является 2-совместимым, для х3, поскольку он — 3-совместимый, и т.д. Для каждой переменной хi необходимо выполнить поиск только среди d значений в ее области определения, чтобы найти значение, совместимое с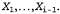Это означает, что гарантируется нахождение решения за время O(nd). Безусловно, за такую возможность также приходится платить: любой алгоритм обеспечения n-совместимости в наихудшем случае должен требовать времени, экспоненциально зависящего от п.