|
Страница 2 из 2 Теперь рассматриваемый интеграл представляет собой обычный интеграл гауссова распределения по всей области его определения, который равен 1. Таким образом, от квадратного уравнения сохраняется лишь его остаточный терм. Вторым важным этапом является преобразование, выполняемое на основе того наблюдения, что остаточный терм должен иметь квадратичную зависимость от  ; в действительности после его упрощения получаем следующее: ; в действительности после его упрощения получаем следующее: 
Таким образом, распределение, прогнозируемое на один этап, представляет собой гауссово распределение с тем же средним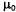 и дисперсией, равной сумме первоначальной дисперсии и дисперсией, равной сумме первоначальной дисперсии и дисперсии перехода и дисперсии перехода . Даже краткие размышления позволяют понять, что такое соотношение интуитивно вполне оправдано. . Даже краткие размышления позволяют понять, что такое соотношение интуитивно вполне оправдано. Для завершения этапа обновления необходимо обусловить вероятность результатами наблюдения на первом временном этапе, а именно z1. Согласно уравнению 15.16, такая операция осуществляется с помощью следующего уравнения: 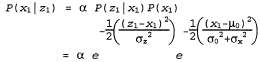
Снова объединим экспоненты и дополним квадрат (упр. 15.6), получая следующее: 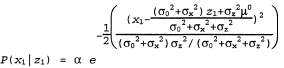 (15.17) (15.17)
Таким образом, после одного цикла обновления будет получено новое гауссово распределение для переменной состояния. На основании гауссовой формулы, приведенной в уравнении 15.17, можно определить, что новые значения среднего и среднеквадратичного отклонения можно вычислить на основе старых значений среднего и среднеквадратичного отклонения следующим образом: 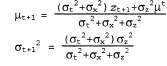 (15.18) (15.18)
На рис. 15.6 показан один цикл обновления для конкретных значений модели перехода и модели восприятия.  Рис. 15.6. Этапы цикла обновления фильтра Калмана для случайного блуждания с априорной вероятностью, заданной параметрами  , шумом перехода, заданным , шумом перехода, заданным =2.0, шумом восприятия, заданным =2.0, шумом восприятия, заданным , и первым результатом наблюдения z1 = 2.5 (это значение показано звездочкой на оси к). Теперь следует отметить, что под влиянием шума перехода предсказание , и первым результатом наблюдения z1 = 2.5 (это значение показано звездочкой на оси к). Теперь следует отметить, что под влиянием шума перехода предсказание сглаживается относительно сглаживается относительно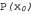 . Заслуживает также внимания то, что среднее апостериорной вероятности . Заслуживает также внимания то, что среднее апостериорной вероятности  находится немного левее от результата наблюдения находится немного левее от результата наблюдения _, поскольку это среднее представляет собой взвешенное среднее от предсказания и наблюдения _, поскольку это среднее представляет собой взвешенное среднее от предсказания и наблюдения Приведенная выше пара уравнений играет точно такую же роль, как и общее уравнение фильтрации, 15.3, или уравнение фильтрации НММ, 15.10. Но в связи с особым характером гауссовых распределений эти уравнения обладают также некоторыми интересными дополнительными свойствами. Во-первых, можно интерпретировать вычисление нового значения среднего как вычисление взвешенного среднего от новых результатов наблюдения как вычисление взвешенного среднего от новых результатов наблюдения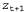 и старого значения среднего и старого значения среднего . Если результаты наблюдения являются ненадежными, то значение . Если результаты наблюдения являются ненадежными, то значение увеличивается и мы придаем больший вес старому значению среднего, а если ненадежно старое значение среднего (велико значение увеличивается и мы придаем больший вес старому значению среднего, а если ненадежно старое значение среднего (велико значение ) или процесс является в высшей степени непредсказуемым (велико значение ) или процесс является в высшей степени непредсказуемым (велико значение ), то придаем больший вес результатам наблюдения. Во-вторых, следует отметить, что обновление для дисперсии ), то придаем больший вес результатам наблюдения. Во-вторых, следует отметить, что обновление для дисперсии 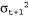 является независимым от результатов наблюдения. Поэтому можно заранее определить путем вычисления, какой должна быть последовательность значений дисперсии. В-третьих, последовательность значений дисперсии быстро сходится к постоянному значению, которое зависит только от является независимым от результатов наблюдения. Поэтому можно заранее определить путем вычисления, какой должна быть последовательность значений дисперсии. В-третьих, последовательность значений дисперсии быстро сходится к постоянному значению, которое зависит только от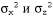 , что способствует существенному упрощению дальнейших вычислений. , что способствует существенному упрощению дальнейших вычислений.
<< В начало < Предыдущая 1 2 Следующая > В конец >>
|