|
В главе 14 было описано ключевое свойство семейства линейных гауссовых распределений: при стандартных операциях в байесовской сети оно остается замкнутым. В этом разделе данное утверждение будет уточнено в контексте фильтрации с помощью временной вероятностной модели. Ниже перечислены требуемые свойства, соответствующие процессу двухэтапного вычисления результатов фильтрации с помощью уравнения 15.3. 1. Если текущее распределение является гауссовым, а модель перехода является гауссовым, а модель перехода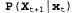 — линейной гауссовой, то распределение, прогнозируемое на один этап вперед, которое задается с помощью следующего уравнения, также представляет собой гауссово распределение: — линейной гауссовой, то распределение, прогнозируемое на один этап вперед, которое задается с помощью следующего уравнения, также представляет собой гауссово распределение: 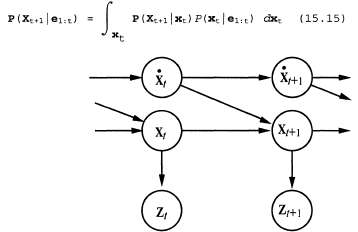 Рис. 15.5. Структура байесовской сети для линейной динамической системы с переменными, определяющими положение скорость скорость и результаты измерения позиции и результаты измерения позиции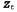 2. Если прогнозируемое распределение является гауссовым, а модель восприятия является гауссовым, а модель восприятия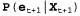 — линейной гауссовой, то после обусловливания вероятности на основании нового свидетельства следующее обновленное распределение также является гауссовым: — линейной гауссовой, то после обусловливания вероятности на основании нового свидетельства следующее обновленное распределение также является гауссовым: 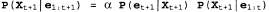 (15.16) (15.16)
Таким образом, оператор Forward для калмановской фильтрации принимает на входе гауссово прямое сообщение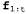 , заданное с помощью среднего , заданное с помощью среднего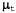 и матрицы ковариации и матрицы ковариации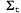 , и вырабатывает новое многомерное гауссово прямое сообщение , и вырабатывает новое многомерное гауссово прямое сообщение 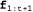 , заданное с помощью среднего , заданное с помощью среднего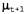 и матрицы ковариации и матрицы ковариации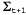 . Итак, начиная с гауссова априорного сообщения . Итак, начиная с гауссова априорного сообщения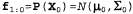 и проводя фильтрацию с помощью линейной гауссовой модели, мы можем получить гауссово распределение вероятностей состояний для любых временных срезов. и проводя фильтрацию с помощью линейной гауссовой модели, мы можем получить гауссово распределение вероятностей состояний для любых временных срезов. Очевидно, что этот научный результат является привлекательным и изящным, но почему он имеет такое важное значение? Причина этого состоит в том, что за исключением нескольких частных случаев, подобных рассматриваемому, в процессе фильтрации с помощью непрерывных или гибридных (как дискретных, так и непрерывных) сетей вырабатываются распределения вероятностей состояний, размеры представления которых растут во времени без ограничения. Это утверждение нелегко доказать, но в упр. 15.5 показано, что в простых примерах так и происходит.
|