|
Страница 2 из 3 Таким образом, задача неконтролируемой кластеризации состоит в восстановлении модели смешанного распределения, подобной приведенной на рис. 20.8, б, из исходных данных, таких как показано на рис. 20.8, а. Очевидно, что если бы мы знали, с помощью какого компонента сформирована каждая точка данных, то было бы легко восстановить гауссово распределение для этого компонента, поскольку можно было просто выбрать все точки данных, соответствующие такому компоненту, а затем применить уравнение 20.4 (вернее, его многомерную версию) для согласования параметров гауссова распределения с множеством данных. С другой стороны, если бы были известны параметры каждого компонента, то можно было бы, по меньшей мере в вероятностном смысле, присвоить каждую точку данных компоненту. Но проблема состоит в том, что не известны ни присваивания, ни параметры. Основная идея алгоритма ЕМ, рассматриваемого в данном контексте, состоит в том, что необходимо принять допущение, будто нам известны параметры этой модели, а затем вычислить вероятность того, что каждая точка данных принадлежит к тому или иному компоненту. После этого нужно снова согласовать компоненты сданными таким образом, чтобы каждый компонент согласовывался со всем набором данных, каждой точке которого назначен вес, соответствующий вероятности того, что она принадлежит к данному компоненту. Такой процесс продолжается итерационно до достижения сходимости. По сути при этом происходит "дополнение" данных путем вычисления распределений вероятностей по скрытым переменным (определяющим, какому компоненту принадлежит каждая точка данных) на основании текущей модели. При использовании смешанного гауссова распределения модель смешанного распределения инициализируется произвольными значениями параметров, а затем осуществляются итерации по описанным ниже двум шагам. 1. Ε-шаг. Вычислить вероятности того, что данные того, что данные были сформированы компонентом i. Согласно правилу Байеса, справедливо соотношение были сформированы компонентом i. Согласно правилу Байеса, справедливо соотношение . Терм . Терм представляет собой вероятность значений данных представляет собой вероятность значений данных в i-м гауссовом распределении, а терм P{C=i) — это параметр определения веса i-гo гауссова распределения; по определению в i-м гауссовом распределении, а терм P{C=i) — это параметр определения веса i-гo гауссова распределения; по определению 2. М-шаг. Вычислить новые значения математического ожидания, ковариаций и весов компонента следующим образом: 
Ε-шаг, или шаг ожидания (expectation), может рассматриваться как вычисление ожидаемых значений скрытых индикаторных переменных скрытых индикаторных переменных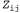 , где значение , где значение равно 1, если данные равно 1, если данные были сформированы i-м компонентом, и 0 — в противном случае. В М-шаге, или шаге максимизации (maximization), осуществляется поиск новых значений параметров, которые максимизируют логарифмическое правдоподобие данных с учетом ожидаемых значений скрытых индикаторных переменных. были сформированы i-м компонентом, и 0 — в противном случае. В М-шаге, или шаге максимизации (maximization), осуществляется поиск новых значений параметров, которые максимизируют логарифмическое правдоподобие данных с учетом ожидаемых значений скрытых индикаторных переменных.
|