|
Страница 1 из 3 Ключевая идея моделей ближайшего соседа состоит в том, что свойства любой конкретной входной точки х, по-видимому, должны быть подобными свойствам точек, соседних по отношению к х. Например, если требуется выполнить оценку плотности (т.е. оценить значение неизвестной плотности вероятности в точке х), то можно просто измерить ту плотность, с какой расположены точки, рассеянные в окрестности х. Такая задача на первый взгляд может показаться очень простой, пока не станет очевидно, что нужно точно определить, что подразумевается под понятием "окрестность". Если окрестность слишком мала, то не будет содержать ни одной точки данных, а если слишком велика, то может включить все точки данных, в результате чего будет получена всюду одинаковая оценка плотности. Одно из возможных решений состоит в том, чтобы определить окрестность как достаточно большую для включения к точек, где к достаточно велико для обеспечения получения осмысленной оценки. При постоянном значении к размеры окрестности изменяются — если данные являются разреженными, то окрестность велика, а если данные расположены плотно, то окрестность мала. На рис. 20.12, а показан пример данных, рассеянных в двух измерениях, а на рис. 20.13 приведены результаты оценки плотности по к ближайшим соседним точкам на основании этих данных при k=3, 10 и 40 соответственно. При к=3 оценка плотности в любой точке основана только на 3 соседних точках и весьма изменчива. При k=10 полученная оценка представляет собой хорошую реконструкцию истинной плотности, показанной на рис. 20.12, б. При k=4 0 окрестность становится слишком большой и информация о структуре данных полностью теряется. На практике хорошие результаты для большинства наборов данных с малым количеством размерностей можно получить с помощью значения k, находящегося примерно между 5 и 10. Подходящее значение для А: можно также выбрать с использованием перекрестной проверки. Для выявления соседних точек, ближайших к точке запроса, нужна метрика расстояний . В двухмерном примере, приведенном на рис. 20.12, используется евклидово расстояние. Но такая метрика становится неподходящей, если каждая размерность пространства измеряет что-то другое (например, рост и вес), поскольку изменение масштаба одной размерности приводит к изменению множества ближайших соседних точек. Одним из решений является стандартизация масштаба для каждой размерности. Для этого измеряется среднеквадратичное отклонение каждой характеристики по всему набору данных и значения характеристик выражаются как кратные среднеквадратичного отклонения для этой характеристики (это — частный случай расстояния Махаланобиса, в котором также учитывается ковариация характеристик). Наконец, для дискретных характеристик можно использовать расстояние Хемминга, в котором . В двухмерном примере, приведенном на рис. 20.12, используется евклидово расстояние. Но такая метрика становится неподходящей, если каждая размерность пространства измеряет что-то другое (например, рост и вес), поскольку изменение масштаба одной размерности приводит к изменению множества ближайших соседних точек. Одним из решений является стандартизация масштаба для каждой размерности. Для этого измеряется среднеквадратичное отклонение каждой характеристики по всему набору данных и значения характеристик выражаются как кратные среднеквадратичного отклонения для этой характеристики (это — частный случай расстояния Махаланобиса, в котором также учитывается ковариация характеристик). Наконец, для дискретных характеристик можно использовать расстояние Хемминга, в котором определяется как количество характеристик, по которым отличаются точки определяется как количество характеристик, по которым отличаются точки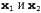
<< В начало < Предыдущая 1 2 3 Следующая > В конец >>
|