|
Страница 1 из 3 По-видимому, числа представляют собой наиболее яркий пример того, как может быть построена крупная теория из крошечного ядра аксиом. В этом разделе будет описана теория натуральных чисел, или неотрицательных целых чисел. Для этого потребуется предикат NatNum, который будет принимать истинное значение при использовании параметра, представляющего собой натуральное число; кроме того, требуется один константный символ, 0, и один функциональный символ, 5 (successor — преемник). Аксиомы Пеано определяют натуральные числа и операцию сложения8. Натуральные числа определяются рекурсивно: 
Это означает, что 0 — натуральное число и для каждого объекта n, если n — натуральное число, S(n) — натуральное число. Поэтому натуральными числами являются 0, S(0), S(S(0)) и т.д. Необходимы также аксиомы для ограничения действия функции определения преемника: 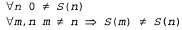
Теперь мы можем определить операцию сложения в терминах функции определения преемника: 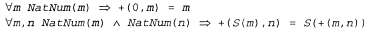
В первой из этих аксиом утверждается, что сложение числа 0 с любым натуральным числом т приводит к получению самого числа т. Обратите внимание на использование бинарного функционального символа " + " в терме + (0, т); в обычной математике такой терм принято записывать в виде 0+т с использованием инфиксной системы обозначений. (Система обозначений, которая используется в этом разделе для логики первого порядка, называется префиксной.) Чтобы было удобнее читать высказывания, касающиеся чисел, здесь будет также разрешено использовать инфиксные обозначения. Кроме того, мы можем записывать как S(n) как п+1, поэтому вторая аксиома принимает следующий вид: 
Эта аксиома сводит сложение к повторному применению функции определения преемника.
<< В начало < Предыдущая 1 2 3 Следующая > В конец >>
|